Artikel ini membahas mengenai Interpolasi Metode Polinomial Orde 2, Orde 3, Orde 4 dimana materi ini akan kalian pelajari pada mata kuliah metode numerik. Sebelum belajar menggunakan program maka sebaiknya kita harus mempelajari terlebih dahulu cara menghitung dengan cara analitis sehingga program dapat dengan mudah dipahami.
Interpolasi Metode Polinomial
Interpolasi adalah cara pendekatan yang fungsinya untuk memprediksi suatu nilai dari beberapa titik yang sudah diketahui. Semakin banyak data diketahui maka hasil dari prediksi akan semakin mendekati hasil yang eksak. Berikut adalah beberapa jenis metode polinomial:
Interpolasi Orde 2
Apabila diketahui ada tiga titik data, untuk memprediksi nilai data maka dapat digunakan interpolasi polinomial orde 2
f2(x) = b0 + b1(x - x0)
+ b2(x - x0)(x - x1)
Dengan nilai koefisien adalah sebagai berikut:
b0 = f(x0)
Interpolasi Orde 3
Interpolasi orde 3 dapat digunakan apabila diketahui terdapat 4 titik data dengan rumus sebagai berikut:
f3(x) = b0 + b1(x - x0) + b2(x - x0)(x - x1) + b3(x - x0)(x - x1)(x - x2)
Dengan nilai koefisien adalah sebagai berikut:
b0 = f(x0)
b1 = f(x1, x0)
b2 = f(x2, x1, x0)
b0 = f(x0)
b1 = f(x1, x0)
b2 = f(x2, x1, x0)
b2 = f(x3, x2, x1, x0)
Dengan nilai fungsi dalam kurung dengan rumus sebagai berikut:
Bentuk Umum Polinomial Orde n
Untuk polinomial orde 4 sampai dst, kalian bisa menggunakan rumus polinomial orde n sebagai berikut ini:
Bentuk umum dari polinomial orde n adalah:
fn(x) = b0 + b1(x-x0) + …… + bn(x-x0)(x-x1)…(x-xn-1)
Dengan nilai koefisien adalah sebagai berikut:
b0 = f(x0)
b1 = f(x1, x0)
b2 = f(x2, x1, x0)
bn = f(xn, xn-1, …………..x1,
x0)
Dengan fungsi dalam kurung merupakan pembagian beda hingga yaitu dengan rumus sebagai berikut:
Pembagian beda hingga pertama adalah:
Pembagian beda hingga kedua adalah:
Pembagian beda hingga ketiga adalah:
Contoh Soal Interpolasi Polinomial
Contoh Interpolasi Polinomial Orde 3
Diketahui 4 titik data yaitu sebagai berikut:
x0 = 1, y0 = 8,345
x1 = 3, y1 = 10,589
x2 = 5, y2 = 13,198
x3 = 5, y3 = 15,869
Jika nilai x adalah 7,5 maka tentukanlah nilai y
Jawab:
Digunakan interpolasi polinomial orde 3
Pembagian beda hingga pertama
Pembagian beda hingga kedua
Pembagian beda hingga ketiga
Hasil dari f[x1,x0], f[x2,x1,x0], f[x3,x2,x1,x0] adalah koefisien dari b1, b2, b3. Dengan b0 = f[x0] = 8,345
f3(x) = b0 + b1(x - x0) + b2(x - x0)(x - x1) + b3(x - x0)(x - x1)(x - x2)
f3(x) = 8,345 + 1,122(7,5 - 1) + 0,0456(7,5 - 1)(7,5 - 3) + -0,006(7,5 - 1)(7,5 - 3)(7,5-5) = 16,533
Contoh Interpolasi Polinomial Orde 4
Jika diketahui:
Carilah nilai y dengan nilai x= 2,4 ,dengan menggunakan interpolasi polinomial order 4
Jawab:
Pembagian beda hingga ketiga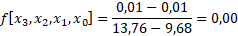
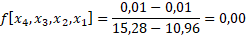
Hasil dari f[x1,x0], f[x2,x1,x0], f[x3,x2,x1,x0], f[x4,x3,x2,x1,x0] adalah koefisien dari b1, b2, b3 dan b4. Dengan b0 = f[x0] = 9,68
f4(x) = b0 + b1(x-x0) + b2(x-x0)(x-x1) + b3(x-x0)(x-x1)(x-x2) + b4(x-x0)(x-x1)(x-x2)(x-x3)
f4(x) = 9,68 + 0,64(x-2) + 0,01(x-2)(x-4) + 0,00(x-2)(x-4)(x-6) + 0,00(x-2)(x-4)(x-6)(x-8) = 9,9296
Baik sekian materi kali ini mengenai Interpolasi Metode Polinomial Orde 2, Orde 3, Orde 4.Setelah mempelajari cara perhitungan metode polinomial secara analitis maka selanjutnya kalian bisa mencoba perhitungan ini dengan menggunakan program.

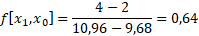
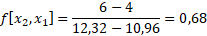

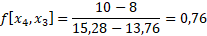
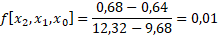



ConversionConversion EmoticonEmoticon