Artikel kali ini akan membahas mengenai Integrasi Numerik Metode Integrasi Trapesium. Metode Integrasi Trapesium dapat dibagi menjadi dua yaitu metode trapesium dengan satu pias dan banyak pias. Pada artikel ini akan dibahas lebih banyak mengenai integrasi numerik metode integrasi trapesium banyak pias dimana dengan semakin banyaknya pias maka hasil akan semakin mendekati nilai eksak.
Metode Trapesium
Metode trapesium adalah salah satu metode pendekatan integrasi numerik dengan cara menjumlahkan segmen-segmen yang berbentuk trapesium.
Metode Trapesium Satu Pias
Pada metode trapesium satu pias, kurva lengkung dari sebuah fungsi f(x) dibuat garis lurus sehingga membentuk bentuk trapesium
 |
| Metode Trapesium satu pias |
Luasan dari bidang tersebut dapat dihitung dengan rumus luas trapesium biasa yaitu:
Metode Trapesium Banyak Pias
Yaitu metode dengan membagi luasan menjadi beberapa pias lalu masing masing pias dibuat bentuk trapesium sehingga dengan semakin banyaknya pias maka hasil yang didapat akan semakin mendekati nilai eksak. |
| Metode Trapesium Banyak Pias |
Luasan dari bidang tersebut dapat dihitung dengan rumus berikut:
Jika dalam perhitungan memperhitungkan koreksi pada ujung interval a dan b, maka persamaan akan menjadi:
Contoh Soal Integrasi Numerik Metode Integrasi Trapesium Banyak Pias
1. Hitung luasan yang dibatasi oleh fungsi f(x) dengan sumbu x antara titik a dan b dengan metode integrasi trapesium dengan banyak pias, persamaan di bawah ini:
f(x) = x3 - 2x2 + 2 dengan (a=0 dan b=4)
Jawab:
Δx = 
Secara Analitis :
y = 29,3333 - 0
y = 29,3333
Dengan Metode Trapesium 8 pias, Maka:
- xo =
0
= 0 => f(xo)
= (0)3 - 2(0)2 + 2 = 2
- x1 =
0 + 0,5 = 0,5 => f(x1) = (0,53 - 2(0,5)2 + 2
= 1,625
- x2 =
0 + 2(0,5) = 1 => f(x2) = (1)3 - 2(1)2 + 2
= 1
- x3 =
0 + 3(0,5) = 1,5 => f(x3)
= (1,5)3 - 2(1,5)2 + 2 = 0,875
- x4 =
0 + 4(0,5) = 2 => f(x4) = (2)3 - 2(2)2 + 2
= 2
- x5 =
0 + 5(0,5) = 2,5 => f(x5)
= (2,5)3 - 2(2,5)2 + 2 = 5,125
- x6 =
0 + 6(0,5) = 3 => f(x6) = (3)3 - 2(3)2 + 2
= 11
- x7 =
0 + 7(0,5) = 3,5 => f(x7)
= (3,5)3 - 2(3,5)2 + 2
= 20,375
- x8 = 0 + 8(0,5) = 4 => f(x8) = (4)3 - 2(4)2 + 2 = 34
Integrasi = 0,5/2 (f(xo) + f(x8) + 2(f(x1) + f(x2) + f(x3) + f(x4) + f(x5) + f(x6) + f(x7))
= 0,5/2 (2 + 34 + 2(1,625 + 1 + 0,875 + 2 + 5,125 + 11 + 20,375)
= 30
Nilai Kesalahan (εa) = 
Bentuk Persamaan Integrasi dengan metode trapesium dengan koreksi:
+f(b)+2\sum_{i=1}^{i=n-1}\right\}-\left\{\frac{\Delta&space;x^2}{12}&space;(f'(b)-f'(a))\right\} "Integrasi Numerik Metode Integrasi Trapesium")
I =
{2+34+(1,625+1+0,875+2+5,125+11+20,375}-
{f'(b)-f'(a)}
I = 30 -{f'(b)-f'(a)}
I =
I = 30 -
Turunan pertama pada ujung
Integrasi:
I = 30 -
(27,25-(-0,75) = 29,416667
(27,25-(-0,75) = 29,416667Nilai Kesalahan (εa) =
= 0,28%2. Hitung luasan yang dibatasi oleh fungsi f(x) dengan sumbu x antara titik a dan b dengan metode integrasi trapesium dengan banyak pias, persamaan di bawah ini:
f(x) = sin 2x - x2 + 2 dengan (a=0 dan b=4)
Jawab:
Δx =
Luas Daerah 1
Luas Total = 1,8804 + 15,0894 = 17,0893
Dengan Metode Trapesium 8 pias, Maka didapat:
- xo = 0 = 0 => f(xo) = sin 2(0) - (0)2 + 2 = 2
- x1 = 0 + 0,5 = 0,5 => f(x1) = sin 2(0,5) - (0,5)2 + 2 = 1,767
- x2 = 0 + 2(0,5) = 1 => f(x2) = sin 2(1) - (1)2 + 2 = 1,034
- x3 = 0 + 3(0,5) = 1,5 => f(x3) = sin 2(1,5) - (1,5)2 + 2 = 0,197
- x4 = 0 + 4(0,5) = 2 => f(x4) = sin 2(2) - (2)2 + 2 = 1,930
- x5 = 0 + 5(0,5) = 2,5 => f(x5) = sin 2(2,5) - (2,5)2 + 2 = 4,162
- x6 = 0 + 6(0,5) = 3 => f(x6) = sin 2(3) - (3)2 + 2 = 6,895
- x7 = 0 + 7(0,5) = 3,5 => f(x7) = sin 2(3,5) - (3,5)2 + 2 = 70,128
- x8 = 0 + 8(0,5) = 4 => f(x8) = sin 2(4) - (4)2 + 2 = 13,860
Integrasi = (f(xo) + f(x8) + 2(f(x1) + f(x2) + f(x3) + f(x4) + f(x5) + f(x6) + f(x7))
= (2+13,86+2(1,767+1,034+0,197+1,930+4,162+6,895+10,128))
= 17,023
Nilai Kesalahan (εa) 
Bentuk Persamaan Integrasi dengan metode trapesium dengan koreksi:
+f(b)+2\sum_{i=1}^{i=n-1}\right\}-\left\{\frac{\Delta&space;x^2}{12}&space;(f%27(b)-f%27(a))\right\} "https://latex.codecogs.com/svg.image?I=\frac{\Delta x}{2}\left\{ f(a)+f(b)+2\sum_{i=1}^{i=n-1}\right\}-\left\{\frac{\Delta x^2}{12} (f'(b)-f'(a))\right\}")
I ={2+13,86+2(1,767+1,034+0,197+1,930+4,162+6,895+10,128)}-{f'(b)-f'(a)}
I = 30 -{f'(b)-f'(a)}
I =
I = 30 -
Turunan pertama pada ujung
Integrasi:
Nilai Kesalahan (εa)
Baik sekian artikel kali ini mengenai integrasi numerik metode integrasi trapesium, tentu materi ini cukup mudah dimengerti bukan?. Cobalah berbagai macam latihan soal mengenai metode integrasi trapesium ini untuk dapat memahami lebih dalam lagi mengenai materi ini.
Blog ini berisi tentang pengalaman saya pada aplikasi untuk mahasiswa teknik sipil
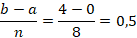
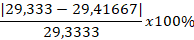
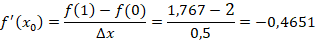
ConversionConversion EmoticonEmoticon